Use thermal analysis to predict an IC‘s transient behavior and avoid overheating
Use thermal analysis to predict an IC's transient behavior and avoid overheating
本文引用地址:http://www.ex-cimer.com/article/163233.htmAbstract:This article presents a method for predicting thermal behavior in ICs. This information will be especially helpful for the PMICs (power-management ICs) used in automotive applications and other high-temperature environments. After characterizing thermal behavior, we formulate a mathematical model that simulates transient temperatures within the chip. We introduce physical laws governing thermal behavior and evaluate them for use in the thermal-body models defined for an IC. Based on that analysis, we then propose an equivalent passive RC network for modeling an IC's transient thermal behavior. To illustrate an application for the proposed analysis, we devise an RC network for an LED driver (the MAX16828). We conclude with insights on the use and usefulness of this approach, and suggest ways to speed the creation of the RC models.
-- ======================================================================= -->-- CONTENT: DB HTML -->-- ======================================================================= -->This article was also featured in Maxim's Engineering Journal, vol. 68 (PDF, 2.72MB).
A similar article appeared in EDN Magazine in January 2010.
Designers often need to know the thermal behavior of an IC, especially for the PMICs (power-management ICs) used in automotive applications. When a particular IC operates at a high temperature (such as +125°C), does it trigger the thermal-shutdown circuitry or exceed the product's safe operating temperature? Without a definite method of analysis, we cannot offer a reliable answer. Therefore, when defining a new IC, we need a way to predict thermal shutdown or excessive die temperature based on complex internal functions.
For operation in DC mode, you can often determine the junction temperature using data-sheet parameters such as θJA (thermal resistance) and θJC (thermal junction temperature).1 However, to predict how high the junction temperature will peak for modes other than DC (such as a power MOSFET driven by a PWM signal to control LEDs or a switching regulator), you need transient thermal data. Although useful, that data is not typically found in data sheets. You might also ask how long the chip can operate at a given power-dissipation level before encountering trouble? That question is also difficult to answer.
This article derives equations that use power dissipation and the ambient temperature to predict the junction temperature of a chip as a function of time. The article begins by introducing the physical laws upon which the analysis is based. The discussion continues by defining an IC system as a complex, layered thermal body. The thermal-body model is then analyzed theoretically, and equations to govern transient thermal behavior are derived. Based on these equations, the article proposes an equivalent RC passive network that represents the IC's thermal characteristics. Finally, to demonstrate the usefulness and accuracy of this analysis, experimental results are shown for a high-voltage, linear HB LED (high-brightness LED) driver with PWM dimming, the MAX16828.
Laws of thermal dynamics
For any object we can derive the required relations for temperature vs. time by using two principal laws.
Newton's law of cooling:
(Eq. 1)
Where:
TB is body temperature.
TA is ambient temperature.
kA is a constant of proportionality (> 0).
t is time.
Law of conservation of nonlatent energy:
(Eq. 2)
Where:
P is constant power generated or imparted to the body.
m is the mass of the body.
c is the specific heat capacity of the body.
Combining these laws, we have:
(Eq. 3)
The data sheet for an IC normally lists thermal data for the package, such as θJA. That data lets us analyze the steady-state thermal equilibrium for a package to see if it agrees with Equation 3:
at the steady state
Therefore:
P = mckA(TB - TA) (Eq. 4)
Equation 4 can be rewritten as:
(Eq. 5)
Where:
θBA is thermal resistance - body to ambient.
TB is the temperature inside the package.
TA is the ambient temperature outside.
Thus:
(Eq. 6)
Defining the chip as a thermal system
A clear definition of the system is very important because the thermal result depends on that definition. In the cross section of a chip mounted on a PCB (Figure 1), we see at least three different materials in the path from die to environment: the die itself, the mold epoxy, and the package. Thermal models are based on one of two patterns of heat flow, depending on the location of the dominant heat source: flow from an external source to the die (when the external source is the dominant heat generator), and flow from the die to the environment (when the die is the dominant heat generator). We will discuss each of these patterns of heat flow in turn.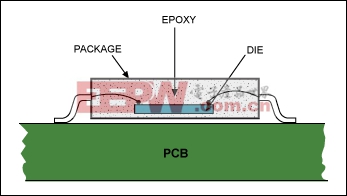
Figure 1. A cross section of a chip mounted on a PCB shows the layers of material between the die and the environment.
Heat flow from an external source to the chip
Consider the system of Figure 2, which shows a uniform body gaining energy (heat) from a power source and losing energy to the environment.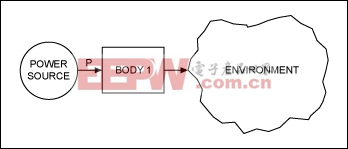
Figure 2. This thermal model illustrates the flow of heat from an outside power source to the chip (BODY 1) and then back out to the environment.
Heat reaches the internal die through the package and the mold compound. Therefore, this system also models thermal transients in the chip for heat sources outside the package. The package normally has a much higher thermal resistance than the die itself because the die has lots of metal on it. The die, therefore, tracks the package temperature with almost no lag, thus causing the chip to behave as a single body. We can define this one-body system immediately by using Equation 3. Solving for TB, we have:
(Eq. 7)
Where ko is the constant of integration, which is solved according to the initial conditions. In general, this equation is useful for defining the thermal transient of a chip when the heat source is outside the chip.
We can illustrate this model with an example. To determine the thermal transient for a chip whose initial temperature is Ti, substitute t = 0 and TB = Ti in Equation 7:
(Eq. 8)
Therefore:
(Eq. 9)
Considering the special case for which Ti = TA:
(Eq. 10)
Using Equation 6, we can rewrite Equations 9 and 10:
(Eq. 11)
(Eq. 12)
Equations 11 and 12 are useful for predicting chip temperature (either package or die) when the heat-generating source is outside the package. One example could be a nearby high-current MOSFET that dissipates lots of heat.
When we know kA and θJA we can calculate the temperature at different times. Alternatively, if P is a complex function of time, we can use the above equations to evaluate temperature as a time-based simulation and use MATLAB® software to write a program that plots temperature as a function of time.
The θJA value is provided in data sheets. However, when a setup imposes conditions other than those of the JEDEC standard, that published θJA value for these calculations can cause errors. The JEDEC standard 51-3 states, It should be emphasized that values measured with these test boards cannot be used to directly predict any particular system application performance, but are for the purposes of comparison between packages.2 Thus, to properly estimate temperature, you should either measure θJA for the prototype board or estimate it directly as explained below.
Heat flow from a die to the environment
Consider the system of Figure 3, in which a three-body system (similar to a chip) generates heat on the die and dissipates it through the epoxy and package to the environment. Body 1 is the die, Body 2 is the epoxy, and Body 3 is the chip package.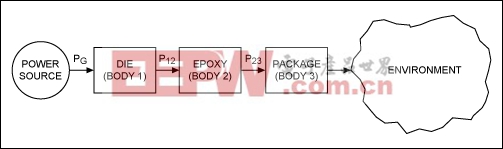
Figure 3. Compare this thermal three-body model with the Figure 2 model. Here the flow of heat generated on the die is more complicated.
To solve for θJA in this system, we must define the equations for all three bodies.
Body 1:
(Eq. 13)
Body 2:
(Eq. 14)
Body 3:
(Eq. 15)
Where:
TB1, TB2, TB3 are the instantaneous temperatures of Bodies 1, 2, and 3.
P12 is power in the form of heat transferred from Body 1 to Body 2.
P23 is power in the form of heat transferred from Body 2 to Body 3.
PG is the power generated on Body 1 or directly transferred to Body1.
Power generated by the die (PG) minus power absorbed by the die is:
(Eq. 16)
Power received by the epoxy minus power absorbed by the epoxy is:
(Eq. 17)
Substituting Equations 16 and 17 in Equations 13, 14, and 15:
(Eq. 18)
(Eq. 19)
(Eq. 20)
The solution of this three-body system in Equations 18, 19, and 20 can be complicated, but the use of Laplace transforms makes it easier. The form of the solution is:
TB1 = T1em1t + T2em2t + T3em3t + TA + (θ12 + θ23 + θ3A)PG (Eq. 21)
Where:
θ12 is the thermal resistance from Body 1 to Body 2.
θ23 is the thermal resistance from Body 2 to Body 3.
θ3A is the thermal resistance from Body 3 to the environment.
T1, T2, and T3 are the constants of integration.
m1, m2, and m3 are functions of k1, k2, and k3.
Equation 21 predicts die temperature in a very accurate way when the die is generating power. To use this equation, however, we must know all the constants of integration plus m1, m2, and m3, which are complicated functions whose solution is difficult. To avoid this difficult exercise, we use a tool for solving differential equations: SPICE.
RC network models thermal-transient differential equations
We will now propose a circuit modeled by similar differential equations, and we will then simulate the circuit and read out temperatures from the simulation.
The differential Equations 18, 19, and 20 can be modeled by a simple RC network (Figure 4) that represents the power generated on the die.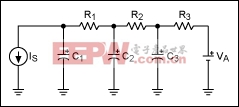
Figure 4. This RC network models the transient-thermal behavior of a chip when heat is generated internally.
In Figure 4 initial voltages on the capacitors represent the initial temperatures of the die (C1), the epoxy (C2), and the package (C3). VA represents the ambient temperature of the environment, and IS (the current going into capacitor C1) represents the power generated on the die. The differential equations representing voltages on the capacitors are:
(Eq. 22)
(Eq. 23)
(Eq. 24)
These three equations correspond to Equations 18, 19, and 20, with the following substitutions of variables:
VC1  TB1, VC2
TB1, VC2  TB2, VC3
TB2, VC3  TB3, lS
TB3, lS  PG
PG
The capacitor voltages correspond directly to the temperatures of the die, epoxy, and package. Any SPICE package can simulate the RC circuit easily. When we know the proper values of R1, R2, R3, C1, C2, and C3 modeled for a particular chip, we can then simulate the circuit and directly read out die temperature as the voltage on capacitor C1.
Now we can determine the passive component values for a particular chip (R1, R2, R3, C1, C2, and C3). Use Equation 5 (repeated below as Equation 25) to obtain the thermal resistance for the system (θJA) by measuring the die's steady-state final temperature:
(Eq. 25)
Where:
TJ is the steady-state junction temperature of the die.
TA is the ambient temperature.
PG is the power dissipated on the die.
Operating with the same dissipated power (PG) as in Equation 25, you can create a data set for the chip's transient temperature variation by measuring the die temperature at different times starting at time 0. Then, based on the following constraint, do a curve-fitting exercise on the measured data to determine the values of R1, R2, R3, C1, C2, and C3:
θJA = R1 + R2 + R3 (Eq. 26)
Measuring the die temperature
There are a couple of practical methods to measure the die temperature of an integrated circuit.3 Here we will use the ESD diode forward-drop measurement method to determine the chip temperature, since it is easy and will not introduce a large amount of error. However, to ensure that the accuracy levels of the measurement remain within acceptable limits, always choose the die-temperature measurement technique for a particular chip carefully. The following guidelines will prove helpful.3
- Make sure that the ESD diode chosen for measurement does not have a large parasitic resistance, nor a large current flow that would offset the diode drop read-out. It is best to discuss this with the IC manufacturer to determine the estimated maximum internal bond-wire and metallization resistance.
- Also make sure that the ESD diode is near the hotspot of the chip or in the area where you are actually concerned with the temperature. This configuration will provide better estimation of the temperature and deliver more accurate results.
- If you are choosing a FET's on-resistance as a temperature indicator, make sure that the FET is fully on and in dropout mode at the measurement point.
To use the ESD diode forward-drop approach, we need a diode on the chip to which we can apply forward bias and measure its voltage. That can easily be done on most chips with an ESD diode connected between a pin and the supply voltage. Because the measured data gives us the diode voltage, we must also consider the relationship between a diode voltage and temperature.4
Diode voltage decreases with a nearly constant slope and negligible deviation. If plotted with respect to temperature, the result would look like the plot in Figure 5.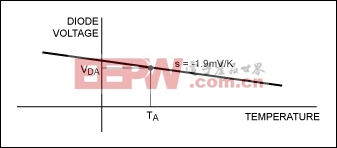



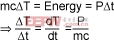
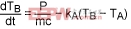
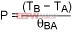


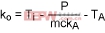
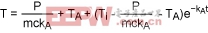
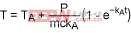
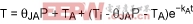

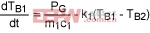
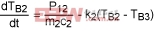
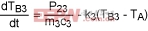
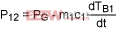
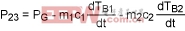
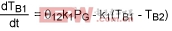
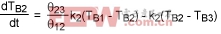
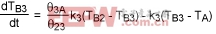

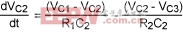
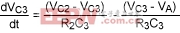
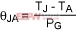








評論